Квадратный корень

Что такое квадратный корень
На самом деле, определение квадратного корня довольно простое.
Квадратный корень — это величина, которая при умножении на саму себя дает исходное число.
Иными словами, мы имеем дело с числом, которое является квадратом другого числа. Если не помнишь, что такое квадрат числа — вот тут у нас есть статья про степени. А извлечение корня — это процесс, обратный возведению в степень. Сам этот процесс извлечения в вычислениях обозначается знаком , внешне отдаленно похожим на приподнятые в недоумении плечи. Под большим плечом записывается величина, которая является квадратом необходимой нам величины.
Пример:
- Возьмем число 9. √9= 3, потому что при умножении 3 на само себя (33) получается 9.
- Аналогично √16 = 4, потому что 42 = 16. Обратный процесс возведению в квадрат — вот и арифметическое определение квадратного корня в самой простой форме.
Извлечение корней
После того как мы поняли, что такое квадратный корень, возникает следующий вопрос — как правильно его находить? Извлечь или найти его можно несколькими способами. Самый распространенный — с помощью калькулятора, но этот трюк на контрольной или ЕГЭ провернуть не получится… Поэтому лучше потренировать свои арифметические мышцы и запомнить квадраты чисел от 1 до 10 (а для сдачи экзамена по профильной математики и до 20). Для больших значений можно обратиться к таблице и подобрать нужное:
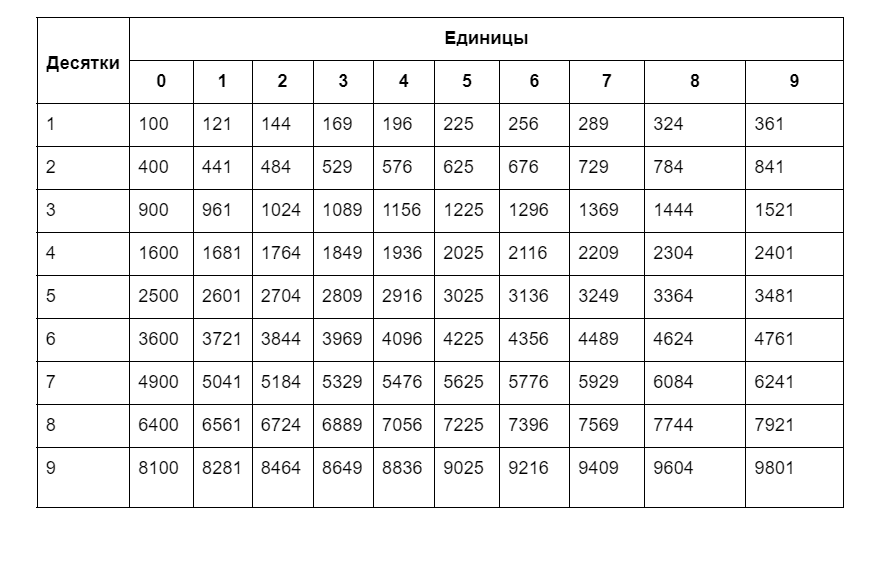
Свойства квадратного корня
Наши товарищи — корни подчиняются своим определенным правилам, или свойствам, которые помогут в дальнейших вычислениях.
Например, квадратный корень из произведения равен произведению квадратных корней.
Пример:
Тот же самый принцип распространяется и на деление. Корень из частного двух чисел равен частному корней этих чисел.
Пример:
Под знаком корня не может находится отрицательное число, поскольку какое число ни возводи в квадрат, отрицательный результат получить невозможно.
Умножение корней
Теперь давай с помощью изученных свойств подробнее остановимся на умножении. Это может быть как и простое, так и более «замысловатое» действие:
Примеры:
Кстати, с дробными числами все это работает точно так же: нам надо найти число, которое при умножении само на себя дает такую дробь. Однако учти, что если под знаком корня может находиться как вся дробь, так и отдельный числитель или знаменатель. Если не помнишь вычисления с дробями — у нас есть отдельная статья.
Примеры:
Деление корней
Ну а теперь рассмотрим деление:
Примеры:
Обрати внимание, что во втором примере корень до конца не извлекся. Так бывает, и паниковать не стоит. Даже если у тебя под корнем в какой—то момент оказывается «не квадрат», то посмотри, не раскладывается ли он на отдельные множители, среди которых квадрат будет. У нас было число 27, которое является 9, умноженной на три, что можно вынести из-под знака корня. Главное в такой ситуации не паниковать и просто перепроверить вычисления.
Возведение в степень
Корень, как и любое другое число, можно возвести в степень. Например, если возвести в квадрат √4, то получится 4, потому что при возведении корня в квадрат мы, по сути, умножаем его на себя, а это дает исходное число. Таким образом (√4)² равно 4, (√10)² равно 10, а (√20)² равно 20.
Внесение под знак корня
А что делать, если под корнем стоит число, которое невозможно получить с помощью возведения в квадрат? Как извлечь неизвлекаемое? В любой непонятной ситуации — вносим число под знак корня, возводя его в квадрат.
Пример:
А если, наоборот, именно под знаком корня оказался «тупик», то можно попробовать вынести из-под него число, представив его в виде произведения отдельных множителей.
Пример:
Сравнение корней
При сравнении корней важно помнить, что чем больше число под корнем, тем больше сам корень. Так, √9 значительнее, чем √4. Аналогично √16 больше, чем √9, а √25 больше, чем √16. Это простое правило, но оно может стать спасательным кругом на уроках алгебры!
Заключение
Ну вот и все! Теперь мы знаем об удивительном мире квадратных корней, их удивительных свойствах и о том, как их вычислять. Мы рассмотрели все — от определений до множества примеров. Сначала, с непривычки, все это может показаться сложным, но главное — помнить, что корни — это как спрятанные сокровища в мире чисел, которые только и ждут, чтобы их открыли.
А если тебе нужно подготовиться к ОГЭ или ЕГЭ по математике, то мы в «Сотке» будем рады тебе помочь. Никакой зубрежки и нудных объяснений — мы достигаем результата через интересные и продуктивные занятия. Не веришь? Тогда записывайся на бесплатный пробный урок и убедись лично. До встречи!
К слову о вычислениях….
Давай повторим новые знания!
Проверь себя
Найди ответ:
- 1785
- 25
- 2704
Найди значение выражения:
- 0,1
- 0
- — 0,1
Выбери наименьшее число:
- √289
- √48 * √3
- √275