Дроби
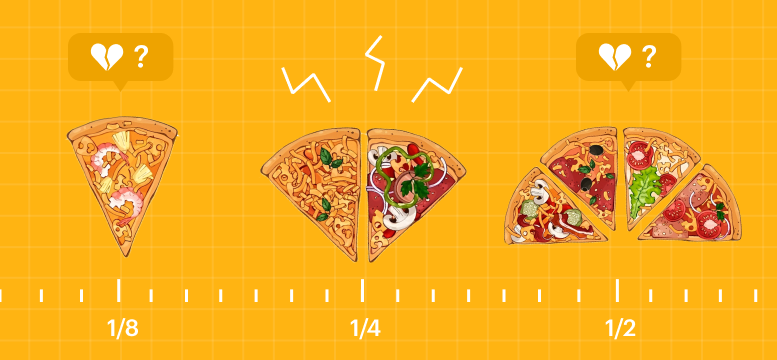
Обыкновенная дробь
Представим какую—нибудь вкусную пиццу или пирог. Пиццу-пирог, чтобы угодить всем. Эту вкусняшку можно поделить на определенное количество ломтиков. Причем здесь дробь?
Обыкновенная дробь — это численное выражение, состоящее из числителя и знаменателя, разделенных чертой. Например, 3/4 или 7/10.
Допустим, что мы решили поделить нашу пиццу-пирог на 4 части, а потом съедим 3 ломтика. Чтобы обозначить количество съеденной пиццы, мы скажем, что уничтожили три четверти, или напишем дробью, что съели 3/4 . Это и будет обыкновенная дробь. По сути в этом выражении зашифровано деление, то есть мы можем представить 3/4 и как 3 ÷ 4, но для работы удобнее именно такая форма:
Числитель — это верхнее число в дроби, которое показывает, сколько частей рассматривается.
Знаменатель — это нижнее число в дроби, которое показывает, на сколько частей разделено целое.
Числитель указывает на количество частей от пиццы-пирога, которые мы кладем себе на тарелку, а знаменатель показывает, на сколько частей наша вкусность делилась.
Важно! Так как в дроби «зашифровано» деление, где знаменатель — это делитель, то согласно старому известному правилу «на ноль делить нельзя» знаменатель не может быть равен нулю.
В a/b знаменатель b ≠ 0
Дроби позволяют представить части целого числа и работать с ними, что делает их очень полезным инструментом для анализа и решения различных задач с пропорциями, простых и рациональных уравнений и вычислений процентов. В повседневной жизни мы тоже постоянно сталкиваемся с ними — например, когда выбираем купить ли 1 литр, 0,75 литра или 0,5 литра сока.
Десятичная дробь
Помимо обыкновенных дробей существуют десятичные. Это когда знаменатель — определенная степень числа 10. Иными словами:
Десятичная дробь — это дробь, которая записывается с помощью запятой (или точки) и основана на делении на десять, сто, тысячу и так далее.
Представим, что наша вкуснейшая пицца — пирог настолько всем понравилась, что мы решили сделать еще одну и пригласить на чай десять человек. Поделив угощение на эти десять частей, мы возьмем себе один кусочек. В «дробной системе» это будет выглядеть как 1/10или 0.1.
Довольно удобно, не так ли? Десятичная дробь — это способ представления дробного числа в десятичной системе счисления. Она состоит из целой части и десятичной части, разделенных точкой. Например, , а
. Десятичная дробь может быть представлена и в виде обыкновенной с помощью деления числителя и знаменателя на одно и то же число. Например, 0.5 = 5/10 = 1/2.
Свойства дробей
У дробей есть важные свойства, которые упрощают вычисления и делают их более доступными. Но для начала вспомним про наш пиццу-пирог:
Допустим, мы решили растянуть удовольствие, и скушать только четверть пиццы-пирога, оставив остальные три четверти на завтра. Но ночью на нас напала страшная тоска и голод, и потому мы съели еще четверть. Что остается в итоге (кроме очевидной зависимости)?
Интересно, что съели мы две четверти, а по факту половину. В математике эта особенность объясняется через следующее свойство:
Если у дроби числитель и знаменатель умножить или разделить на одно и то же число, то получится дробь, равная исходной.
Пример:
Знаменатель дроби не может быть равен нулю, так как делить на него нельзя
Эти свойства значительно упрощают вычисления и сводят к минимуму ошибки. Дроби и работа с ними необходимы в алгебре, тригонометрии и базовых вычислениях.
Действия с дробями
Что же за базовые вычисления? Действия с дробями включают сложение, вычитание, умножение, деление и сокращение.
1. Сокращение: для того чтобы сократить дробь, нужно разделить и числитель, и знаменатель на одно и то же число. Нужно это для того, чтобы упростить работу с числами. Гораздо же проще работать с , чем с
, верно? Для сокращения нужно подобрать наибольший общий делитель (НОД) числителя и знаменателя.
Пример:
можно сократить до
, разделив числитель и знаменатель на 5.
2. Сложение и вычитание: складывать или вычитать можно только дроби с общим знаменателем. Для этого необходимо умножить каждую дробь на число, которое сделает их знаменатели одинаковыми. Только после можно складывать или вычитать числители, сохраняя знаменатель неизменным.
Пример:
3. Умножение: для проведения умножения дробей следует перемножить между собой их числители и знаменатели.
Пример:
4. Деление: разделить одну дробь на другую можно, умножив одну из них на обратное число другой. Обратное число — это число, которое при умножении на данное число даёт единицу. Найти его очень просто — переставь числитель и знаменатель местами, и вуаля!
Пример:
Заключение
Так что вот они, дроби: важный инструмент в математике, который помогает нам работать с числами и пирогами. Понимание обыкновенных и десятичных дробей, их свойств и того, как с ними работать, — ключ к успеху в математике и жизни. Но перед тем как бежать заказывать пиццу, давайте…
Проверим себя!
Проверь себя
Какое из следующих выражений соответствует значению 1/4?
- (1/2) / (1/2)
- (1/2) * 2
- (1/2) * (1/2)
Какой наименьший общий знаменатель (НОД) у 2/3 и 1/4?
- 12
- 16
- 24
Какая из следующих дробей является результатом действия (1/3 + 0,4)?
- 11/15
- 7/30
- 17/30