Степень числа

Понятие
Степень числа — это многократное умножение числа на себя. Количество умножений указывается в показателе степени. Число, которое умножается — в основании степени.
Если у нас есть степень а с показателем n, который больше единицы, то это выражение записывается как an,(а в степени n).
Возвести в степень — значит, взять какое-то число, и умножить его само на себя какое-то количество раз. Сколько раз ты будешь производить умножение — показывает показатель степени. Он потому так и называется — показатель, легко запомнить. А число, которое мы будем умножать, называют основанием степени.
Математически определение можно записать так:
где:
a — основание;
n — показатель.
Непонятно? Сейчас будет проще.
Помнишь Наруто? Представь, что он может создавать копии самого себя, но последовательно. То есть сначала Наруто создает одну копию самого себя — как бы умножает себя на 2. А потом оба этих Наруто снова создают по копии — опять умножают себя на 2. И снова, и снова, и снова… И так — 8 раз.
Сколько у нас будет Наруто?
Чтобы решить это, нам нужно будет взять 2 и умножить её саму на себя 8 раз. Получится 2*2*2*2*2*2*2*2.
Длинно. И запутаться при счете легко: одну двойку пропустили — и уже результат неправильный.
Поэтому умные математики придумали записывать это иначе. Цифру 2 мы взяли 8 раз. И получили 2 в степени 8 — 28
Эта запись читается как «2 в степени 8» или «8-ая степень числа 2»
С показателями степени 2 и 3 все еще проще.
Если показатель степени равен 2 — с2 — запись читается как «с в квадрате»;
Если показатель равен 3 — с3 — читаем как «с в кубе».
Легко запомнить: когда мы умножаем число само на себя, мы как бы находим площадь квадрата со стороной, равной этому числу. Поэтому a2 — «а в квадрате».
А если мы умножаем число само на себя трижды, то как будто находим объем куба. Поэтому a3 — «а в кубе».
А теперь еще немного всё упростим.
Степенью числа «а» с показателем n = 1 является само это число:
a1 = a
Почему? Потому что мы не умножали число, мы просто взяли его 1 раз.
Как Наруто, который не применял никаких техник.
Ноль в любой натуральной степени равен нулю.
0n = 0
Вообще просто: сколько на 0 не умножай — все равно получится 0.
Единица в любой степени равна 1.
1n = 1
С единицей та же история: умножать её можно сколько угодно, больше она не станет.
Любое число в нулевой степени равно единице.
a0 = 1
Объяснение этой истории будет чуть ниже.
Теперь разберемся с положительными и отрицательными числами.
ab = с
c больше 0, если:
- a больше 0
- a меньше 0, но b — четное
c меньше 0, если a меньше 0, и b — нечетное
Если мы возводим в степень положительное число (больше нуля) — мы всегда получаем положительное число.
С отрицательными числами (меньше нуля) всё интереснее.
Если показатель степени четный — после возведения в степень получится положительное число. Помнишь, минус на минус даёт плюс? С четным показателем степени все отрицательные числа встают в такие пары. Это как на медляке: все разбиваются на пары, никто не остается обиженным.
(-2)6= -2 * -2 * -2 * -2 * -2 * -2 = 4*4*4 = 64
Если показатель степени нечетный — результат возведения в степень отрицательного числа будет также отрицательным числом.
По той же логике. Минус на минус дает плюс, а вот плюс на минус — минус.
С нечетным показателем степени наши отрицательные числа не делятся на ровные пары, и остается одинокая цифра, которая всем портит медляк.
(-2)7= -2 * -2 * -2 * -2 * -2 * -2 * -2 = 4*4*4*(-2) = -128
Таблица степеней
Это штука, в которой можно посмотреть степени чисел от 1 до 10. Как таблица умножения, только таблица степеней.
Как пользоваться: в левом столбце находишь число, с которым будешь проводить операцию. В верхней строке — ту степень, в которую число надо возвести. Ищешь ячейку пересечения — и вуаля! — результат.
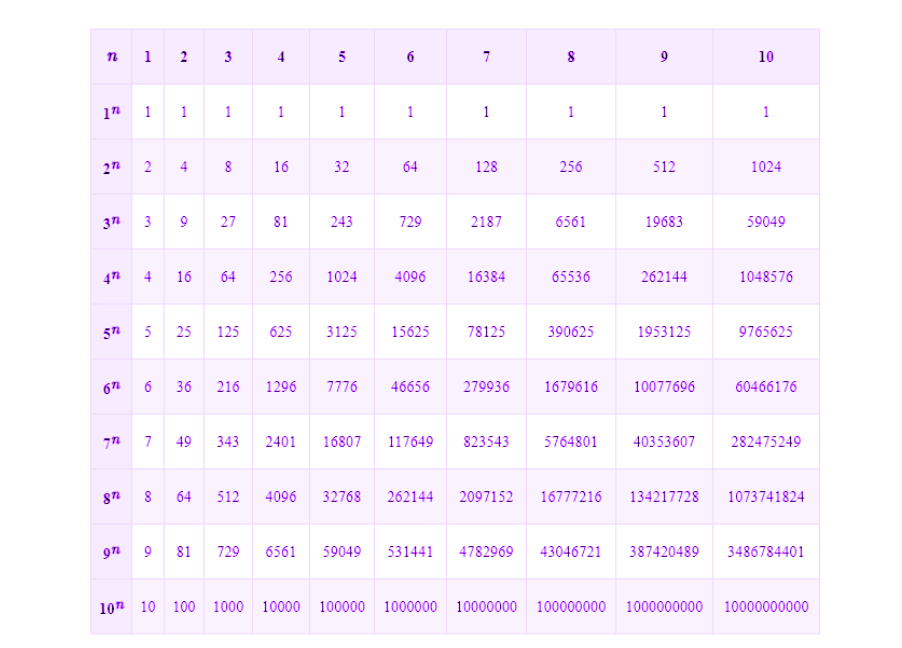
Пример:
Нам нужно узнать 4 в степени 6.
Находим в левом столбце 4, в верхней строке — 6, мысленно пересекаем линии. На пересечении — 4096, это наш результат.
Свойства
Свойства степеней — это, по сути, правила, по которым мы будем считать числа в степенях.
Свойство 1: произведение степеней
Если мы умножаем степени, у которых основание одинаковое, то основание мы не трогаем. Берем показатели степеней и складываем их.
an * am = am+n
a — основание степени
m, n — показатели степени, любые натуральные числа
Пример:
45 * 42 = ?
Видим одинаковое основание — 4. Оставляем его в покое и складываем показатели степени: 5 и 2. Получаем выражение 45 * 42 = 45+2 = 47 = 16384
Свойство 2: частное степеней
Допустим, нам надо поделить степени с одинаковым основанием. Тогда само основание мы не трогаем, а показатели вычитаем: из показателя делимого показатель делителя.
an / am = am-n
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Кстати, это свойство объясняет, почему a0 = 1. Чтобы получить показатель степени 0, вам нужно вычесть показатель степени из самого себя, то есть поделить число само на себя: аn : аn = аn-n = а0 = 1.
Пример:
45 / 42 = ?
Видим одинаковое основание — 4. Его не трогаем, вычитаем показатели степени: 5 и 2. Получаем выражение 45 / 42 = 45-2 = 43 = 64
Свойство 3: возведение степени в степень
Основание остается неизмененным, а показатели умножаются друг на друга.
(an)m = an·m
a — основание степени
m, n — показатели степени, натуральное число
Пример:
(45)2 = ?
Основание — 4 — пусть остается. А показатели 5 и 2 перемножаем. Получаем выражение (45)2 = 45*2 = 410 = 1048576
Свойство 4: возведение в степень произведения
Возводим в степень каждый множитель, затем перемножаем полученные результаты.
(a * b)n = an * bn
a, b — основания степени
n — показатели степени, натуральное число
Пример:
(4 * 2)2 = ?
Основания — 4 и 2 — каждое возводим в степень. И затем перемножаем полученные результаты. Получаем выражение 42 * 22 = 16*8 = 128
Свойство 5: возведение в степень частного
Возводим в степень делимое и делитель по отдельности, а затем производим, собственно, деление.
(a / b)n = an / bn
a, b — основание степени, b ≠ 0,
n — показатель степени, натуральное число
Пример:
(4 / 2)2 = ?
Основания — 4 и 2 — каждое возводим в степень. И затем первый результат делим на второй. Получаем выражение 42 / 22 = 16/8 = 2
Сложение и вычитание
Тут все просто. Начинаем с возведения в степень, а с плюсами и минусами разбираемся потом. Если есть скобки — начинаем с них.
Пример:
45 – 62 = ?
Скобок нет, поэтому сначала возводим 4 и 6 в степени, затем выполняем вычитание. Получаем: 45 – 62 = 1024 – 36 = 988
(4 – 6)5 = ?
Скобки есть, поэтому сначала выполняем вычитание, а потом уже результат возводим в степень. Получаем: (4 – 6)5 = (-2)5 = -32
Обрати внимание: основание степени — отрицательное число, а показатель — нечетное, следовательно, мы однозначно получим в ответе отрицательное число!
Проверь себя
Как будет выглядеть запись этого выражения с использованием степеней? 5*5*5*5 – 4*4*4 / 2*2
— 45 – 46 / 26
— 54 – 43 / 22
— 24-3 / 62
Чему будет равно выражение y∙y∙y3∙y2
— y7
— y5
— 6y
4 ∙ 8 ∙ 32 = ?
— 45
— 210
— 960