Признаки делимости

Понятие делимости
Представь, что у тебя есть 6 конфет и 4 друга, с которыми ты хочешь поделиться поровну. Попробуй выделить каждому 2 конфеты — для этого 2 надо умножить на 4. Получается, что тебе нужно 8 конфет. Что-то не то, да?
А вот если бы у тебя был пятый друг — например тот, который все равно съест только одну конфету, — задача стала бы проще. К сожалению, жизнь такова, что все хотят конфет и равенства. Поэтому требуется подключать извилины и выворачиваться.
Пусть каждый получит всего по одной конфете. 1 умножить на 4 логично даст 4 конфеты. Но тогда у тебя останется 2 лишних конфеты. Что это значит? Тут в игру вступает понятие делимости!
Делимость — это свойство, которое позволяет определить, делится ли одно число на другое нацело, то есть без остатка.
Например, если 12 делится на 3, то результат — 4 и остатка не будет. Но если ты попытаешься разделить 12 на 5, то получится 2 и сверху останется 2 (остаток).
В случае с конфетами, число 6 никак не делится на 4, потому что получается остаток в виде двух конфет. Если бы тебе изначально пришлось распределять их между 3 друзьями, то все бы получили по 2 конфеты и у тебя бы не осталось лишних.
В математике, особенно когда говорим о делимости, чаще всего имеется в виду работа с натуральными числами. Натуральные числа — это те, которые мы используем для счета: 1, 2, 3, 4 и так далее. Давай посмотрим, как можно по простым правилам определить, делится ли число на другие.
Признаки делимости
Кажется, задачка с конфетами довольно неудобная. Сидишь, подбираешь и умножаешь — скука та еще. Хорошо, что в математике есть простые признаки деления, которые помогают определить, делится ли число на 2, 3, 5 и другие. Для этого необязательно выполнять деление полностью — достаточно знать несколько правил. Вот основные признаки для самых популярных случаев:
1) Делимость на 2: Чтобы узнать, делится ли число на 2, достаточно взглянуть на его последнюю цифру. Если число заканчивается на 0, 2, 4, 6 или 8, оно будет делиться на 2, потому что это признак четности.
Пример: 24 заканчивается на 4, а значит, будет делиться на 2.
2) Делимость на 3: Чтобы понять, может ли число делиться на 3, сложи все его цифры и посмотри, можно ли разделить эту сумму на 3.
Пример: У числа 123 сумма цифр будет 1 + 2 + 3 = 6. 6 делится на 3, значит, 123 тоже.
3) Делимость на 9: Аналогично с 3, если сумму цифр числа можно разделить на 9, то и само число тоже будет делиться на 9.
Пример: 27, 2+7=9, а значит, что 27 можно поделить на 9.
4) Делимость на 5: Все числа, которые оканчиваются на 0 или 5, делятся на 5.
Пример: 45 оканчивается на 5, значит, разделится на 5 без остатка.
5) Делимость на 10: Если число оканчивается на 0, оно делится на 10.
Пример: 130 оканчивается на 0, значит, делится на 10.
А если запомнить эти правила, можно поражать друзей «ментальными фокусами»: «Эй, Вася, 123 456 делится на 3?» — а ты уже знаешь ответ!
Таблица признаков делимости
В математике часто используют таблицы, чтобы наглядно представить основные признаки делимости:
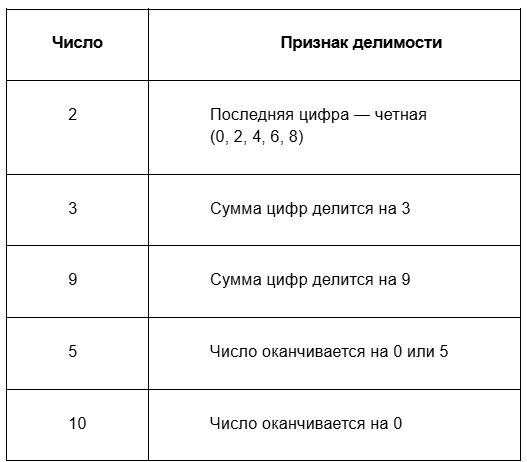
Почему математики так любят признаки делимости? Потому что это магия — произнес пару цифр и готово! Никаких долгих вычислений, путаницы и бесконечных делений столбиком. Очень изящно!
Заключение
Теперь ты знаешь основные правила и признаки делимости чисел. С их помощью можно быстрее решать задачи и понимать, на какие числа делится нужное тебе значение. Если тебе нужно быстро проверить, делится ли какое-то число, вспомни признаки и таблицу. Математика становится проще, когда знаешь такие маленькие, но полезные секреты!
А пока давай проверим новые знания!
Проверь себя
1) Как понять, что число можно поделить на 9?
- Сумма цифр числа делится на 9
- Сумма цифр числа дает 9
- Число оканчивается на 9
2) На какое число нельзя разделить 246?
- 3
- 5
- 2
3) Выбери лишнее:
- 203004
- 81
- 143