Параллелограмм: свойства и признаки

Определение параллелограмма
Параллелограмм — это четырехугольник с двумя парами параллельных сторон. Противоположные стороны параллелограмма имеют равную длину, а его противолежащие углы всегда равны.
Частными случаями параллелограмма, кстати, являются давно нам знакомые квадрат, ромб и прямоугольник. Параллелограммы часто используются в геометрии, а еще они применяются в различных направлениях науки — например, в инженерии, архитектуре и физике.
Свойства параллелограмма
Параллелограмм — это не просто красивая фигура. Он, как и другие геометрические фигуры, обладает рядом свойств — которые, кстати говоря, нам было бы очень полезно знать, чтобы легко (и безболезненно) решать задачи на ЕГЭ.
Так вот, свойства параллелограмма:
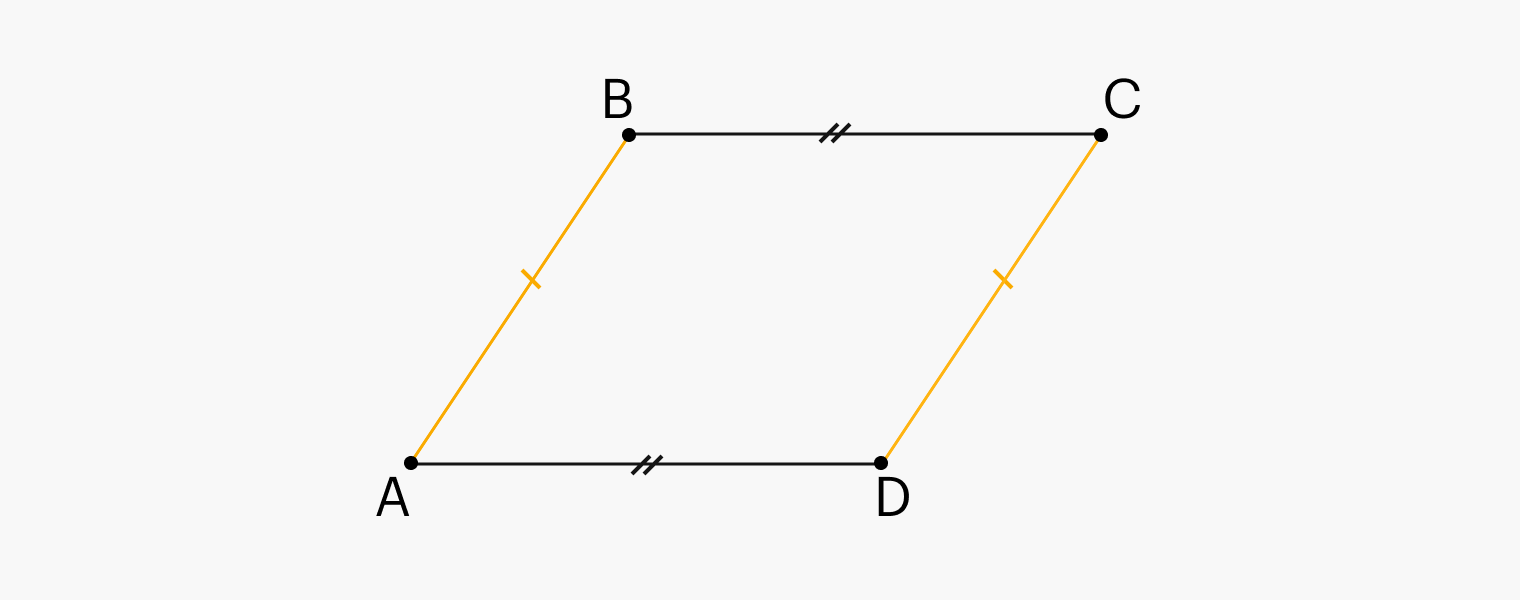
- Противоположные стороны параллелограмма параллельны: они имеют одинаковую направленность и не пересекаются.
- Противоположные стороны параллелограмма равны: длина параллельных сторон одинакова.
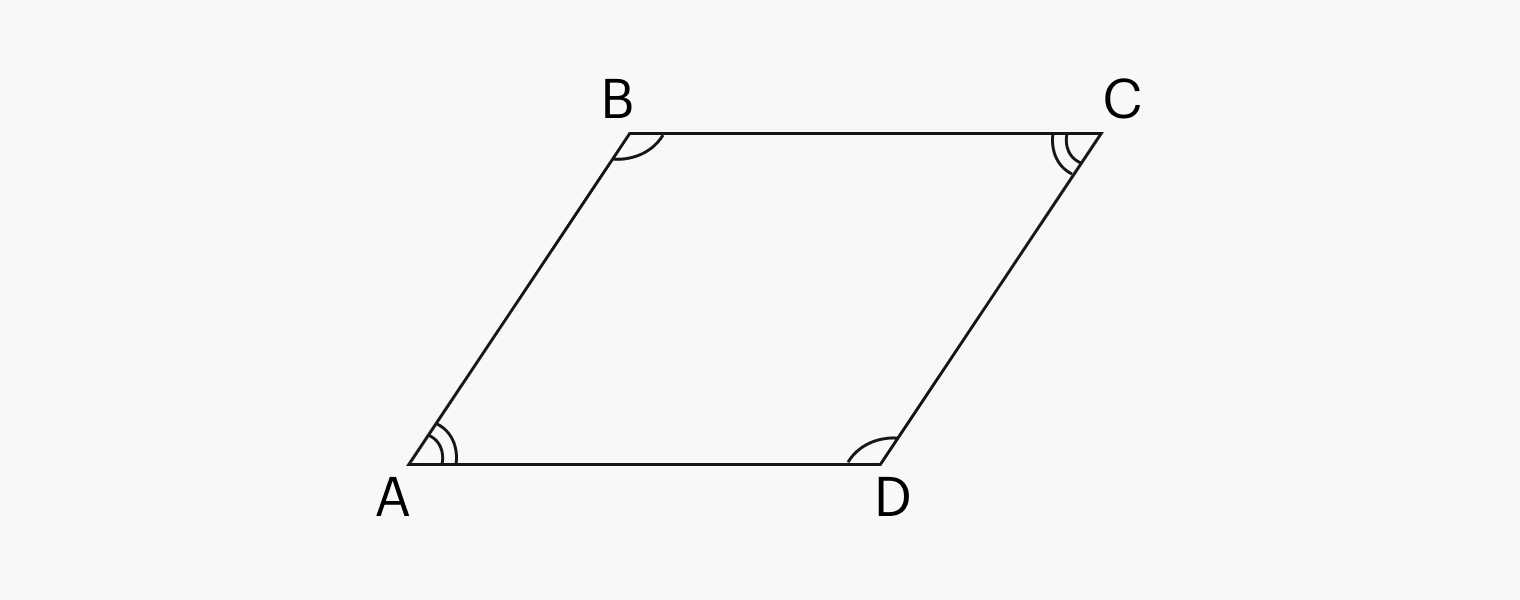
- Противоположные углы параллелограмма равны.
- Соседние углы параллелограмма дополнительны, то есть сумма смежных углов равна 180 градусам.
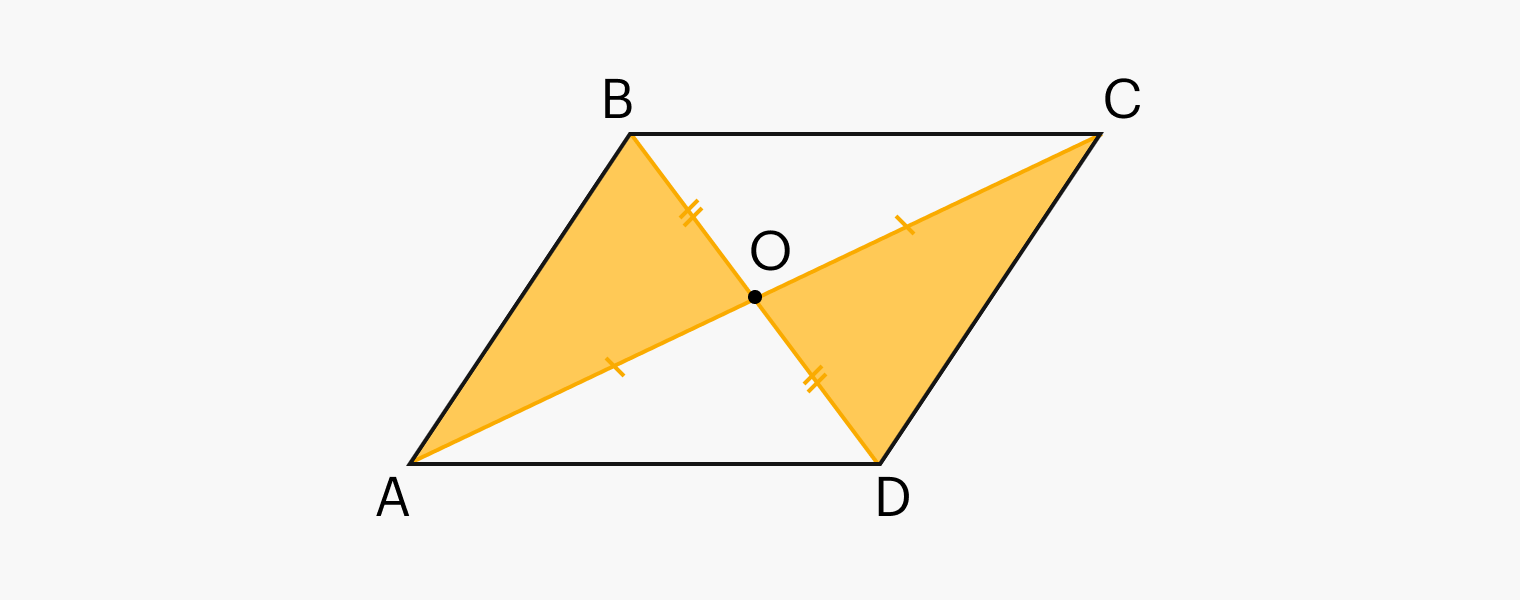
- Диагонали параллелограмма делятся пополам в точке пересечения.
- Точка пересечения диагоналей — это центр симметрии параллелограмма.
- Диагональ делит параллелограмм на два равных треугольника.
Эти свойства могут использоваться для решения задач на нахождение углов параллелограмма, длины сторон и площади, диагоналей и высоты параллелограмма.
Признаки параллелограмма
Признаки — это то, что отличает параллелограмм от других геометрических фигур. То есть, это условия, которые должны выполняться, чтобы конкретная фигура являлась параллелограммом.
Четырехугольник ABCD является параллелограммом, если:
(здесь картинка параллелограмма с диагоналями и другая с обозначением углов)
1) Противоположные стороны одновременно равны и параллельны друг другу
AB = CD, AB || CD.
2) Противоположные углы попарно равны
∠A = ∠C, ∠B = ∠D.
3) Диагонали параллелограмма делятся пополам в точке пересечения
AO = OC, BO = OD.
4) Противоположные стороны попарно равны
AB = CD, AD = BC.
5) Противоположные стороны попарно параллельны
AB || CD, AD || BC.
Если одно из этих условий выполняется (а в этом случае выполняются и другие условия), то фигура является параллелограммом. Значит, любой из этих признаков мы можем использовать для доказательства.
Площадь и периметр параллелограмма
Площадь параллелограмма можно найти несколькими способами — в зависимости от того, какие данные о фигуре у нас есть, а каких не хватает.
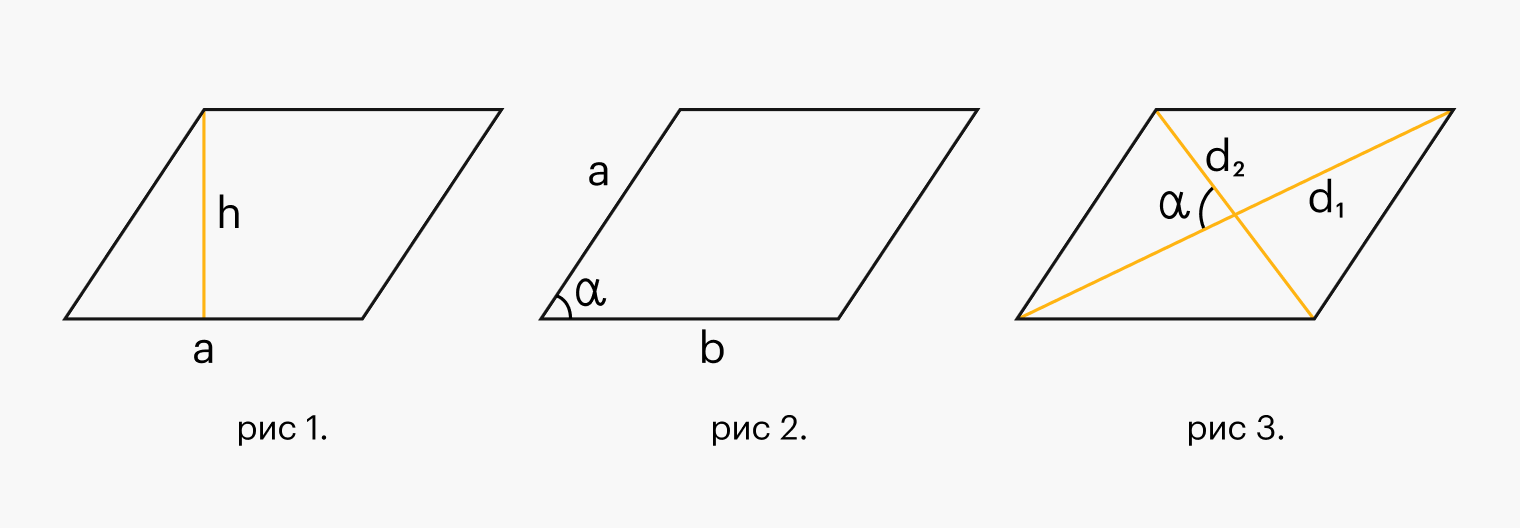
Если известны длины одной стороны и основания (рис. 1), опущенного к этой стороне, то площадь будет равна произведению этих длин.
S = a * h,
где S — площадь, a — длина одной из сторон, h — высота, опущенная на эту сторону.
Если известны длины обеих сторон и угол между ними (рис. 2), то можно вычислить площадь как произведение длин этих сторон, умноженное на синус угла между ними.
S = a * b * sin(α),
где S — площадь, a и b — длины сторон, α — угол между этими сторонами.
Если известны только длины диагоналей параллелограмма (рис. 3), то тоже есть возможность определить его площадь. Она будет равна половине произведения длин диагоналей, умноженной на синус угла между ними.
S = (d1 * d2 * sin(α)) / 2,
где S — площадь, d1 и d2 — длины диагоналей, α — угол между диагоналями.
С периметром параллелограмма все проще — он вычисляется как сумма длин всех сторон фигуры:
P = 2a + 2b,
где P — периметр параллелограмма, a и b — длины параллельных сторон.
Зная площадь и периметр параллелограмма, можно решать различные задачи, связанные с этой фигурой, — например, находить длины сторон или углов, находить площадь или периметр при изменении размеров и прочее.