Натуральные числа

Определение натурального числа
Начнем, как полагается, с самого начала. Итак,
Натуральное число — это любое положительное целое число. То есть оно больше нуля и не имеет дробной части.
1, 24, 567, 124856 — все это примеры натуральных чисел (далее — н.ч.). Используются они для базовых вычислений, счета и определения порядка. Множество н.ч.обозначается в математике буквой N. Первое из них равно 1, а следующие идут по порядку: 2, 3, 4 и так далее до бесконечности, образовывая цепочку чисел,у которой в математике есть свое определение:
Натуральный ряд – это последовательность натуральных чисел, начинающаяся с 1 и продолжающаяся бесконечно: 1, 2, 3, 4 и так далее, как, например, на этой таблице:
Свойства натуральных чисел
Область математики, в «юрисдикции» которой находятся натуральные числа, называется арифметикой. Да-да, та самая «добрая» математика из начальной школы, когда мы считали, сколько баночек варенья съел пушистый лисенок. Но возвращаемся из полей ностальгии в наши суровые реалии и запоминаем основные свойства н.ч.:
- Натуральные числа подчиняются коммутативному закону, что означает, что сумма не изменится, даже если мы изменим порядок цифр. Например, 4 + 3 – это то же самое, что и 3 + 4.
- Аналогично при умножении порядок множителей не влияет на произведение. Так, н.ч. 4, умноженное на 5, равно 5, умноженной на 4.
- Существует также ассоциативный закон для сложения. Это означает, что когда у нас есть несколько членов, результат сложения не зависит от порядка действий. Например, (2 + 3) + 4 — даст тот же результат, что и 2 + (3 + 4).
- Тот же самый принцип распространяет и на умножение. Если в произведнии есть несколько членов, то порядок умножения не повлияет на результат. Так, (6 7) 8 даст тот же результат, чтои 6 (7 8).
- Натуральные числа подчиняются распределительному закону. Для умножения суммы на число мы можем умножить на него каждый член и сложить результаты. Так, 4 (5 + 6), равно (4 5) + (4 6). А при делении распределительный закон гласит, что для того чтобы разделить сумму на н.ч., нужно разделить на него каждый член и сложить результаты. Так, (9 + 8)3, — это то же самое, что (93) + (83).
Разряды и классы
Начнем с основ. Есть числа, а есть цифры. Числа — это то, чем мы пользуемся при счете. А цифры — это те знаки, которыми мы числа записываем. Разделение их на разряды и классы помогает лучше понять, как читать и записывать многозначные числа.
Разряды – это позиции цифр в числе, каждая из которых показывает количество единиц определённого порядка.
Примеры разрядов: единицы, десятки, сотни. Например, в числе 125 цифра 1 относится к разряду сотен, цифра 2 — к разряду десятков, а цифра 5 — к разряду единиц.
Классы – это группы разрядов, объединяющие цифры для удобства чтения больших чисел.
Например, класс единиц содержит единицы, десятки и сотни, класс тысяч – тысячи, десятки тысяч и сотни тысяч, класс миллионов – миллионы и так далее.
Разделяя многозначные числа на классы, читать их становится проще. Каждый класс представляет собой группу из трёх цифр, и значение классов увеличивается по мере продвижения слева направо.
Чтобы прочитать натуральное число 744333590179, выделим классы таким образом: 744 333 590 179. Теперь прочитаем число слева направо: 744 миллиарда, 333 миллиона, 590 тысяч, 179 (слово «единицы» в большинстве случаев опускается).
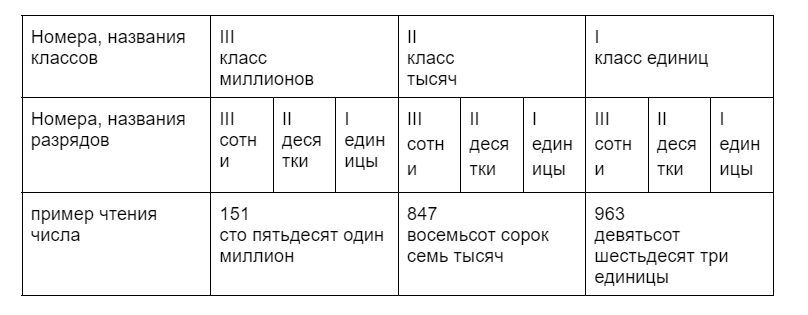
Давай составим таблицу, чтобы лучше понять классы и разряды на примере н.ч. 151 847 963:
Заключение
Что ж, подведем итог: натуральные числа очень важны для математики. Они как строительные блоки для многих математических концепций и вычислений. Понимание их свойств, разрядов и классов помогает нам производить не только базовые вычисления, но и весьма сложные действия.
К слову о понимании…
Проверь себя
Какое число можно назвать натуральным?
- простое, целое
- рациональное, положительное
- положительное, простое
Сколько всего классов и разрядов в 154073607?
- 3 класса и 9 разрядов
- 4 класса и 3 разрядов
- 5 классов и 6 разрядов
Какое из этих чисел натуральное?
- 27, 5
- 1034
- -8