Метод интервалов — это самый простой и универсальный способ решения квадратных неравенств, экономящий много времени на контрольных и экзаменах. Или, как говорят математики,

Метод интервалов — это алгоритм решения дробно-рациональных неравенств, основанный на разделении числовой прямой на интервалы. При этом интервалом называется промежуток той же числовой прямой, ограниченный двумя числами.

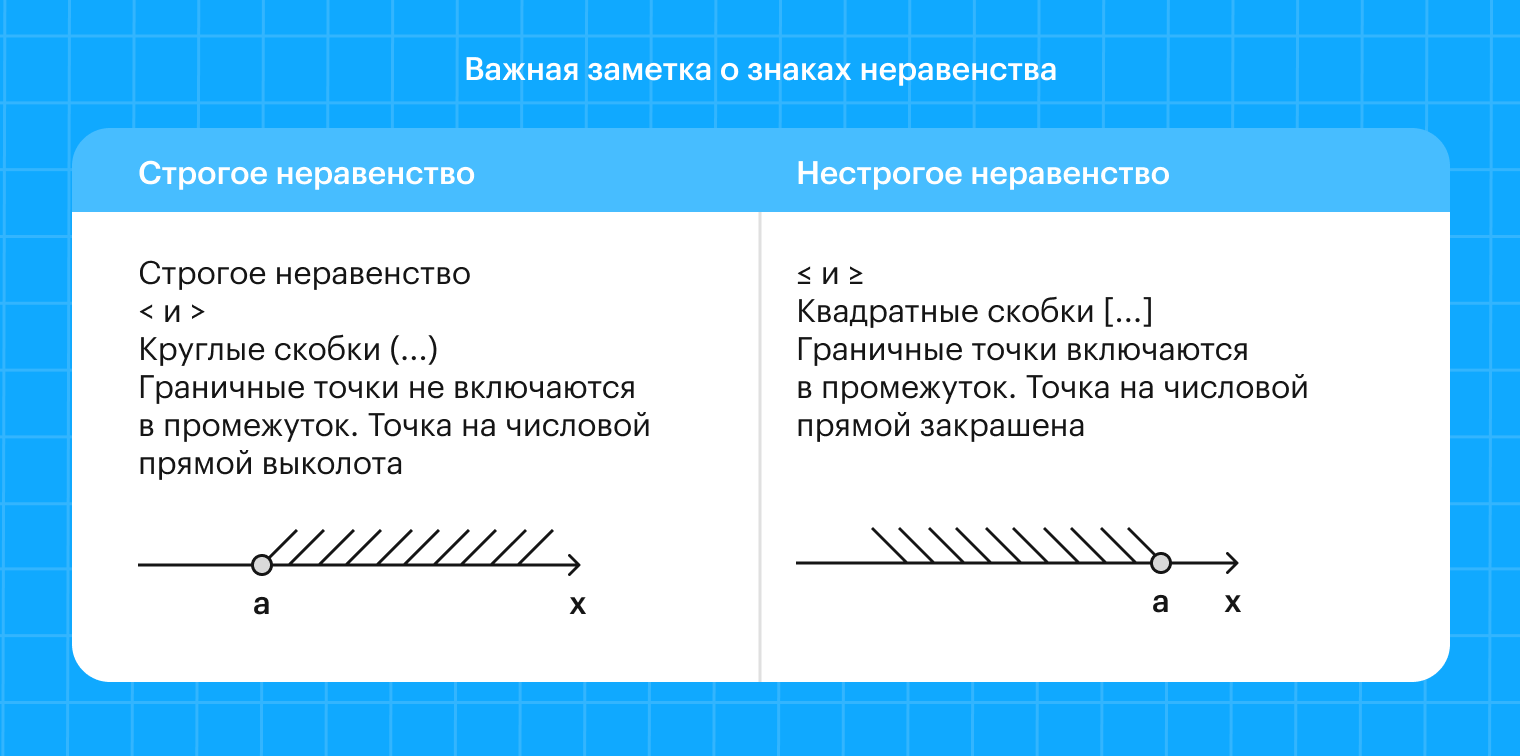
Этот способ можно использовать при решении неравенств с любыми знаками. Неважно, какая изогнутая фигурка разделяет две части выражения: < или >, ≤ и ≥ — все это не имеет значения. А вот что действительно важно, так это то, что степень выражения должна быть второй или выше.

А еще для того, чтобы воспользоваться этим методом, придется прощупать в себе творческую жилку. Иначе как мы будем рисовать по несколько интервальных промежутков для каждого неравенства? Готовь карандаш и бумагу, так как чертить нужно будет достаточно много. 

Давай внесем в эту работу немного креатива и узнаем, как применять метод интервалов в настоящих математических задачках.

Сначала составим пошаговый план, которого нужно придерживаться при использовании метода интевалов на числовой прямой.

1. Если необходимо, привести неравенство к стандартному виду, то есть сделать так, чтобы все кучи цифр, иксов, скобок, плюсов и минусов остались в левой части, а ноль — в правой.
2. Найти нули функции из левой части, то есть решить уравнение f(x) = 0 и найти корни.
3. Построить числовую прямую и отметить на ней полученные корни, выбрав при этом подходящий вид точек — выколотые или закрашенные.
4. Определить знаки на каждом из интервалов, подставив подходящие значения х в исходное выражение.
5. Вернуться к неравенству и выбрать нужный промежуток значений на числовой прямой.
6. Записать ответ.

Ну что, составили план, теперь попробуем применить его в решении настоящих заданий! Предупреждаем: здесь очень легко запутаться, упустить какой-то из этапов, потерять минус или неправильно определить нужные промежутки. Так что последнее наставление: старайся быть внимательнее.

Возьмем следующее математическое выражение:

Шаг 1. Привести к стандартному виду

Это уже сделано, выражение изначально в стандартном виде: ноль справа, все остальное — слева. Можно спокойно переходить ко второму этапу.

Шаг 2. Найти нули функции

В этом пункте нам важно найти значения функции х. Значит, нужно решить уравнение (х – 6) (3х – 15) = 0.

Решение:

1) х – 6 = 0 → x = 6,

2) 3x – 15 = 0 → 3x = 15 → x = 5.

В итоге получилось два корня: 5 и 6. Записываем их и идем дальше — они как раз пригодятся в следующем пункте.

Шаг 3. Построить прямую и отметить на ней нули функции

Мы построили числовую прямую Х и отметили на ней две точки: 5 и 6, которые получили при решении уравнения. Точки выколоты, потому что неравенство в условии задания строгое (со знаком >). 

Получилось три интервала: 

1. от минус бесконечности до 5, 
2. от 5 до 6,
3. от 6 до плюс бесконечности. 

Шаг 4. Определить знаки интервалов

Чтобы определить знаки промежутков, нужно подставить числа в исходное выражение и посчитать, что получится. 

Начнем с первого интервала: он принимает значения от –∞ до 5. Если, например, х = 1, то (х – 6) (3х – 15) = (–5) * (–12) = 5 * 12 = 60. Результат положительный, следовательно, знак этого промежутка «+».

Переходим к следующему интервалу: от 5 до 6. Возьмем значение х равное 5,5. Тогда (х – 6) (3х – 15) = (–0,5) * 1,5 = –0,75. Результат отрицательный → ставим знак промежутка «–».

И последняя дуга: от 6 до +∞. Подставляем х = 10, получаем (х – 6) (3х – 15) = 4 * 15 = 60. Значение выражения положительное, значит ставим знак «+». 

А затем нужно перенести описанное выше на наш рисунок. Отмечаем промежутки на числовой прямой х, а затем рисуем небольшие дуги, соединяющие выколотые точки. И вот что получится.

Шаг 5. Выбрать промежуток на числовой прямой

Вспоминаем, как выглядело неравенство, данное в условии задания: (х – 6) (2х – 5) > 0. 

Выражение слева строго больше нуля, значит и на числовой прямой нам подходят только интервалы со знаком «+». Выбираем их и записываем решение: х принадлежит отрезкам от минус бесконечности до 5 и от 6 до плюс бесконечности. 

Только на языке математики это предложение будет выглядеть так: х ∈ (–∞; 5) U (6; +∞). Символ ∈ означает принадлежность, а перевернутая вниз дуга, похожая на английскую букву U, показывает объединение промежутков.

Вот мы и закончили — это была основная информация, которую нужно знать о методе интервалов и его применении при решении рациональных неравенств. Давай проверим, что получилось запомнить из этой статьи!

Что из этого присуще строгому неравенству?

— Выколотые точки на числовой прямой.

— Квадратные скобки.

— Знаки ≤ и ≥.

(х – 10) = (50х + 5). Что не так с этим неравенством?

— Оно не приведено к стандартному виду.

— В нем слишком большие значения х.

— Это не неравенство.

Какой из предложенных ответов будет верным для следующего выражения? 

— х ∈ [–0,5; +∞).

— х ∈ (–∞; –0,5].

— х ∈ [–2; 2].