Таблица производных функций

Что такое производная функции и как ее найти?
Сразу предупредим, в заданиях ЕГЭ по профильной математике есть вопросы, связанные с исследованием функций, и там таблица производных тебе о-очень пригодится! А еще, заглядывая вперед, скажем, что нужно будет знать правила дифференцирования, и о них мы тоже расскажем в этой статье. Так что подключаем внимание и впитываем знания.
Начнем с определения, чтобы сразу стало понятно, с чем мы имеем дело.
Производная функции — это особый математический инструмент, который позволяет нам понять, как быстро меняется значение функции в определенной точке при изменении ее входных данных.
Опять звучит сложно? Не переживай, сейчас разберемся на примере.
Представь, Дима решил готовиться к математике, и в первый месяц это давалось ему тяжело, он занимался максимум 30 минут и уставал. Но он изучил основы, и со второго месяца начал заниматься каждый день на 5 минут больше.
То есть в первый месяц никакого прогресса по времени не было (значение было константой), и скорость прироста была нулевой. В таблице (обязательно покажем её, но чуть позже) мы найдем, что производная константы равна 0.
f(x) = 30
f’(x) = 0
А вот со второго месяца Дима стал увеличивать время на подготовку на 5 минут каждый день, начиная с 30 минут.
f(x) = 30 + 5x
В той же таблице мы найдем, что производная от x будет равна 1.
f’(x) = 0 + 5
f’(x) = 5
Итак, мы доказали, что время на подготовку Димы росло со скоростью 5 минут в день. В этом и есть суть производной.
Таблица производных — это удобная схема, которая помогает нам понимать, как функции меняются.
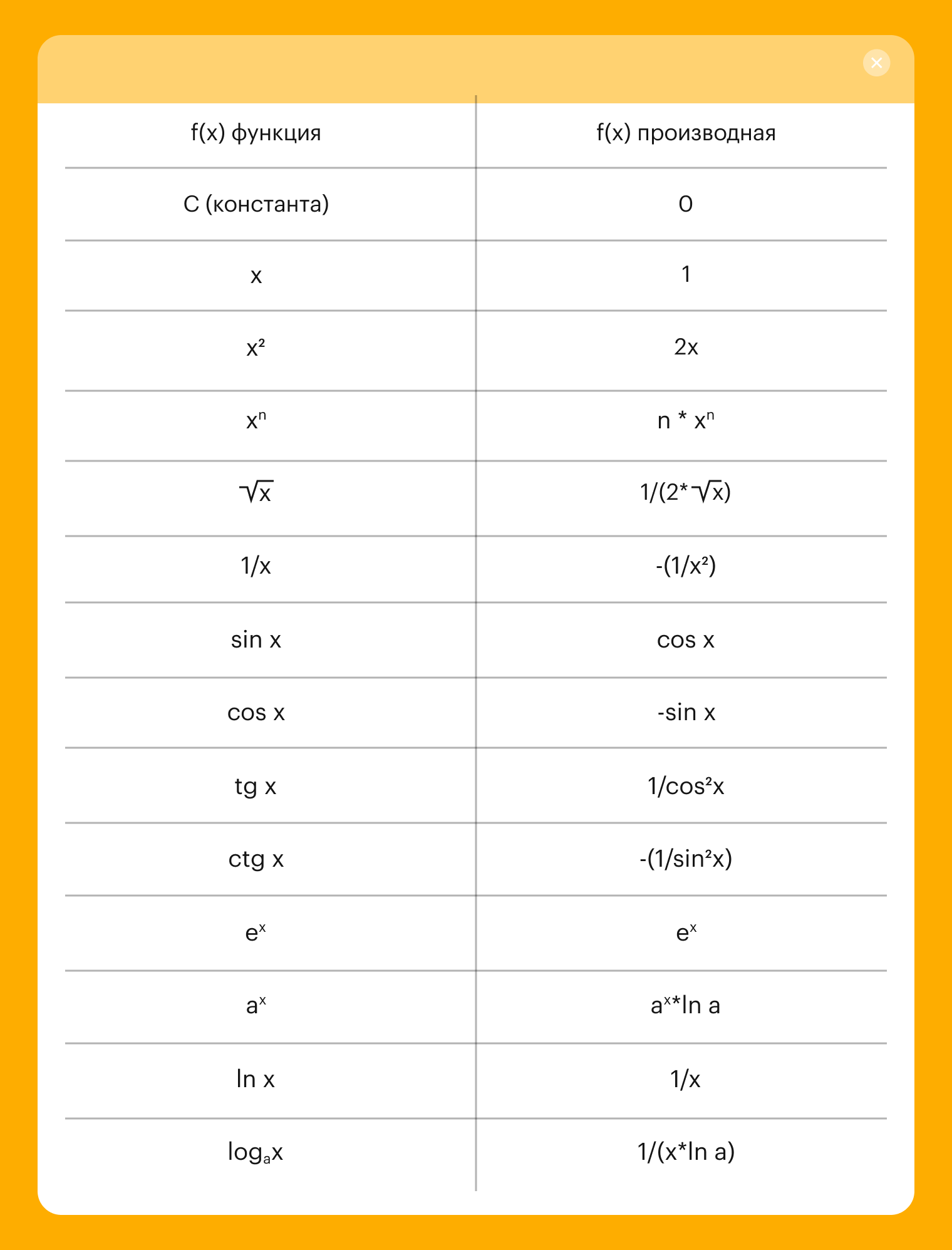
Найти производную функции — это, по сути поиск ответа на вопрос, насколько быстро что-то меняется. И, собственно говоря, страшное дифференцирование — ничто иное, как процесс поиска производной! Уже не так и страшно, правда? А теперь попробуем разобраться, как ее найти.
Правила дифференцирования функций
Поговорим о правилах дифференцирования. Это набор формул и приемов, которые помогут нам находить производные легко и просто.
Примем, что f(x), g(x) — это функции, C — постоянное число (константа), и посмотрим, что придумали ученые, чтобы упростить нам жизнь:
1. Для константы: если у нас есть постоянное число C, то будет работать (с * f(x))’ = c * f’(x), то есть константу мы выносим за скобку.
2. Для суммы: (f(x) + g(x))’ = f’(x) + g'(x).
3. Для разности: (f(x) - g(x))’ = f’(x) - g'(x).
4. Для произведения: (f(x) * g(x))’ = f'(x) * g(x) + f(x) * g'(x).
5. Для частного: (f(x) / g(x))’ = [f'(x) * g(x) - f(x) * g'(x)] / [g(x)]2.
Посмотрим, как это работает!
Примеры решений
Рассмотрим несколько примеров.
1.Предположим, у нас есть f(x) = (4 * х2), и мы хотим найти её f'(x).
Применим правило константы: f'(x) = 4 * (х2)’ = 4 * 2 * x2-1 = 8x.
2.Предположим, у нас есть g(x) = 4/x, и мы хотим найти её g'(x).
Применим правило частного: g'(x) = [0 * x - 1*4] / x2 = -4/x2.
Мы изучили, что такое производная функции и как ее находить, используя дифференцирование. Эти знания могут пригодиться в разных областях: от физики до экономики.
Проверь себя
Что такое производная функции?
- Скорость изменения значения функции в конкретной точке.
- Математическая загадка.
- Максимальное значение функции на заданном участке.
Правило дифференцирования для произведения производных.
- f’(x) + g'(x).
- f’(x) - g'(x).
- f'(x) * g(x) + f(x) * g'(x).
Какая производная соответствует функции f(x) = (х + х4)?
- f’(x) = 0.
- f’(x) = 1 + 4x3.
- f’(x) = 2x4.