Двоичная система счисления

Что такое двоичная система счисления и как ей пользоваться?
Двоичная (бинарная) система счисления — это система записи чисел, в основании которой всего два символа: 0 и 1
Эту систему придумал еще в 18 веке немецкий ученый Готфрид Вильгельм Лейбниц. А в начале 20 века Клод Шеннон ввёл понятие «бит» — минимальное количество информации:
0 — ложь — нет тока (0 бит);
1 — истина — есть ток (1 бит).
С тех пор двоичную (бинарную) систему счисления стали использовать все ЭВМ, в том числе и современные компьютеры.
Из плюсов: таким способом закодировать можно все, что угодно. Из минусов — кодирование выглядит как огромный массив и занимает очень много места.
Свойства чисел в двоичной системе счисления
Чтобы упростить себе жизнь и вычисления, запомни несколько свойств бинарных чисел.
- Все числа двоичной СС начинаются с 1
- Если число заканчивается 0 — оно четное, 1 — нечетное
- Любые степени двойки можно записать в двоичной системе как 1 и n-ное количество 0, которое равно степени: 2n = 1 и n нулей.
Примеры:
32 = ?2
35 — это пятая степень двойки, то есть в бинарной записи пишем 1 и 5 нулей: 32 = 25 = 1000002
128 = ?2
128 — это седьмая степень двойки, то есть в бинарной записи пишем 1 и 7 нулей:
128 = 27 = 100000002
- Числа вида 2n–1 можно записать n-ным количеством единиц: 2n–1 = n единиц
Пример:
31 = ?2
31 — это 32-1, а 32 — это пятая степень двойки, то есть в бинарной записи для 31 пишем просто 5 единиц.
31 = 25 – 1 = 11111
- Если известна двоичная запись числа A, то для двоичной записи числа 2А достаточно приписать к записи числа А ноль в конце.
Пример:
11=10112, 22 = ?2
Мы знаем бинарную запись числа 11, это 10112. 22 = 2*11, то есть в бинарной записи мы можем просто приписать ноль в конце: 22 = 101102. Аналогично для 44, 88 и так далее: 44 = 1011002 , 88 = 1011002
- Если число А находится в интервале 2n-1 А < 2n,в его двоичной записи будет только n цифр.
Пример:
Сколько цифр в бинарной записи числа 529?
Вспоминаем степени двойки. Число 519 находится в интервале между 512 и 1024: 29 519 < 210. То есть в его бинарной записи будет 10 цифр: 519 = 10000001112
А еще нам нужно разобраться в развернутой форме записи числа.
Любое число в двоичной СС можно записать в развернутой форме с помощью степени соответствующего разряда и основания степени (основание счета).
Вообще-то это можно в любой системе счисления делать (как — мы писали вот тут)
Развернутая форма записи числа в любой позиционной системе счисления выглядит так:
Aq = an-1 * qn-1 + an-2 * qn-2 + an-3 * qn-3 …+ a0 * q0 …+ a-m * q-m
Что есть что в этой страшной формуле?
A — само число (то, что нам надо развернуть)
q — основание системы счисления (то, сколько символов в алфавите)
ai — цифры нашего числа по порядку записи
n — количество разрядов целой части числа
m — количество разрядов дробной части числа (если она есть)
Кажется, сложно? А ведь это почти начальная школа!
Да-да, в начальной школе мы все это уже делали.
Нас просили записать число 345 развернуто, и мы писали 345 = 300 + 40 + 5.
Но постой-ка… Ведь мы уже знаем, что такое степень числа! Поэтому смело можем записать это иначе:
345 = 3*102 + 4*101 + 5*100
Видишь сходство с той страшной записью выше? Мы уже делали развернутую запись в десятичной СС. А сейчас разберемся, как сделать это в двоичной.
Примеры:
Записываем развернуто 1011012
Наше A = 101101, q = 2, n = 6 (так как у нас 6 цифр в числе).
Чтобы не запутаться, сразу пронумеруем разряды:
Записываем:
1011012 = 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20
Теперь пробуем записать развернуто 11002
Наше A = 1100, q = 2, n = 4 (так как у нас 4 цифры в числе).
Чтобы не запутаться, сразу пронумеруем разряды:
Записываем:
1011012 = 1*23 + 1*22 + 0*21 + 0*20
Как переводить бинарные числа в десятичные и шестнадцатеричные
Самый простой способ любого перевода из одной СС в другую — воспользоваться калькулятором перевода (благо, в сети их хватает). Минус у этого решения один, но очевидный: на контрольных и экзаменах пользоваться таким способом не получится.
Поэтому разберем, как делать все это ручками.
Перевод в десятичную СС.
Алгоритм максимально простой, если уже освоена развернутая форма записи.
- Берем бинарное число
- Записываем его в развернутой форме
- Считаем получившийся результат (умножаем и суммируем то, что у нас в развернутой записи получилось)
Примеры:
Нужно перевести в десятичную систему 1011012
Записываем в развернутой форме и выполняем вычисления:
1011012 = 1*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 4510
Перевод в шестнадцатеричную СС.
Чтобы перевести бинарные числа в шестнадцатеричную систему, можно воспользоваться тремя способами:
- Самый муторный. Выполнить перевод в два действия: сначала перевести в десятичную, а потом уже из десятичной в шестнадцатеричную. Это долго и есть высокий шанс запутаться и ошибиться. Поэтому…
- Упрощенный по алгоритму:
- Разбиваем двоичное число на группы по 4 цифры справа налево (на тетрады);
- Если в самой левой группе (последней) не хватет цифр, доставляем вместо недостающих первых цифр нули (перед остальными цифрами);
- В каждой полученной группе умножаем каждый разряд на 2n, где n — номер разряда;
- Получившиеся результаты записываем в том же порядке, заменяя цифры после 9 на соответствующие буквы латинского алфавита — это и будет число в шестнадцатеричной СС.
Пример:
110102 = (0001) (1010) = (0*23 + 0*22 + 0*21 + 1*20) (1*23 + 0*22 + 1*21 + 0*20) = (0+0+0+1) (8+0+2+0) = (1) (10) = 1A16
- Упрощенный для тех, у кого хорошая память (или учителя разрешают использовать дополнительные материалы). Так же делим число в двоичной системе на четверки (тетрады). А затем просто подставляем нужные значения из вот этой таблицы:
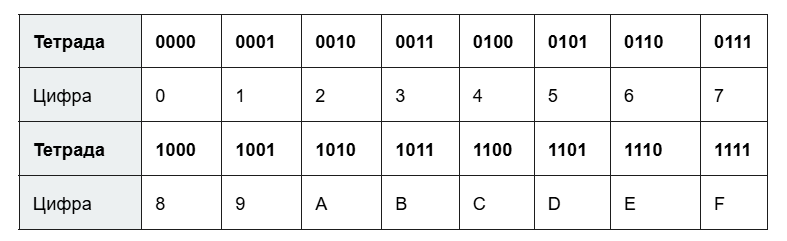
Пример:
1011111002 = (0001) (0111) (1100) = 17C16
Как переводить десятичные числа в бинарные
Чтобы преобразовывать в бинарную СС из десятичной, нам потребуется такой навык, как деление столбиком.
Алгоритм преобразования на диво прост:
- Берем десятичное число
- Делим его на основание нашей СС — на 2.
- Получившиеся в процессе деления остатки записываем в обратном порядке
Пример:
Нам нужно перевести 5610 в двоичную систему счисления:
Для начала берем 56 и делим на основание желаемой системы, у нас это 2.
56 / 2 = 28 и остаток 0
28 / 2 = 14 и остаток 0
14 / 2 = 7 и остаток 0
7 / 2 = 3 и остаток 1
3 / 2 = 1 и остаток 1
1 / 2 = 0 и остаток 1
Теперь все остатки записываем в обратном порядке: 5610 = 1110002
Проверь себя
1. В каком ряду все представленные числа — четные?
— 11101002, 101002, 1101012
— 10110102, 11110102, 1010102
— 110112, 1001102, 1100112
2. Сколько значащих нулей в двоичной записи числа 63?
— 3 нуля
— 6 нулей
— нет нулей
3. Переведи десятичное число 123 в двоичную и шестнадцатеричную СС. В какой строке верно указаны оба результата?
— 11110112, 7B16
— 1001102, 8F16
— 10101102, 24B16