Дизъюнкция

Что такое дизъюнкция
Помнишь, с чего начиналась математика? Мы учились складывать, ведь это самое простое из всех действий. В логике тоже есть сложение — это дизъюнкция, одна из простейших операций. Но здесь не получится сложить 2 и 2 и получить 4. Несмотря на то, что операция называется сложением, работает это сложение иначе.
Дизъюнкция — это логическая операция, которая объединяет два высказывания и возвращает значение истины, если хотя бы одно из этих высказываний истинно.
То есть в логике мы эти высказывания складываем, чтобы получить новое высказывание, которое будет соответствовать хотя бы одному из поставленных условий или сразу двум.
Для обозначения операции в логике приняты такие слова «OR» и «ИЛИ», а также символы «∨», «|» и «+». В программировании используется еще один вариант обозначения, но об этом мы поговорим позже. Эти символы пригодятся тебе на экзамене, чтобы обозначить дизъюнкцию или распознать ее среди других операций. Так что запомни их.
Для всех операций в логике используют таблицы истинности. Соединяя выражения, мы хотим получить результат, и таблицы истинности показывают, что нам ждать от этого результата. Он может оказаться истинным и ложным. На экзамене нужно будет уметь их применять и читать. О таблицах истинности у нас есть статья.
Задачи, в которых для решения нужно применить дизъюнкцию, есть и в ОГЭ, и в ЕГЭ. Давай разбираться, как это все работает, чтобы не ошибаться на экзамене.
Пример
Нужно выбрать, для какого из вариантов будет ложным высказывание (x > 8) ИЛИ (x = нечетное число):
- x = 42.
- х = 4.
Перед нами операция дизъюнкции, значит, ложным высказывание может быть в одном случае: когда оба условия окажутся ложными. Проверим оба варианта.
- x = 42
(41 > 8) — истина.
(42 — нечетное число) — ложь.
Результат логического сложения истинный, когда выполняется хотя бы одно условие. Как мы видим, выполняется первое условие 42 больше 8. Значит, x = 42 — истина.
- x = 4
(4 > 8) — ложь.
(4 — нечетное число) — ложь.
Оба условия ложные, значит, высказывание x = 4 — тоже ложное.
А теперь мы перенесемся в мир разных логических систем и посмотрим, как можно применить дизъюнкцию в каждой из них.

Классическая логика
Классическая или бинарная логика — это система логики, основанная на двух бинарных значениях: истина и ложь. То есть каждое утверждение может быть однозначно определено как истинное или ложное.
Пример
Утверждение «Солнце встает на востоке» — истинно, а утверждение «Солнце встает на западе» — ложное.
Как видно из примера, классическая логика не предполагает никаких других вариантов, кроме как истина и ложь.
В классической логике дизъюнкция — это бинарная операция, которая объединяет два или более логических высказывания в одно.
Дизъюнкция обозначается символом «∨» и ее результат истинный в двух случаях:
- Если хотя бы одно из высказываний, объединенных дизъюнкцией, является истинным.
- Если все высказывания, объединенные дизъюнкцией, являются истинными.
Если все высказывания ложны, результат дизъюнкции будет ложным.
Пример:
Событие А — это высказывание «Сегодня солнечный день».
Событие В — это высказывание «Сегодня идет на пляж».
Если сегодня солнечный день, то дизъюнкция «A ∨ B» будет истинной, даже если мальчик не идет сегодня на пляж.
Если сегодня облачный день и мальчик не идет на пляж, то результат дизъюнкция будет ложной.
Дизъюнкция «A ∨ B» в классической логике будет истинной, если хотя бы одно из утверждений верно.

Булева алгебра
Булева алгебра — это дисциплина, которая изучает логические выражения и операции над ними. В отличие от обычной арифметики булева алгебра работает с двумя значениями: истиной (True) и ложью (False), которые также могут быть представлены числами 1 и 0 соответственно.
Дизъюнкция (OR) — это одна из основных логических операций булевой алгебры, объединяющая два или более логических высказывания.
Дизъюнкция в булевой алгебре будет истинной, если оба или хотя бы одно из логических высказываний, объединенных дизъюнкцией, является истинным.
Пример
Утверждение А: «Ты будешь готовиться к информатике».
Утверждение В: «Ты будешь готовиться к физике».
Объединяем эти два утверждения с помощью дизъюнкции: Ты будешь готовиться к информатике OR Ты будешь готовиться к физике.
Предположим, что ты очень хочешь поступить на айтишника, тогда ты будешь готовиться к информатике (A = True), но на всякий случай решил подготовиться и к физике (B = True), и результат дизъюнкции будет истинным: True OR True = True.
Но может быть ты будешь готовиться к только информатике (A = True), а вот к физике ты готовиться не собираешься (B = False), и тогда объединив эти два утверждения мы все равно получим истину: True OR False = True.
А вот если ты не будешь готовиться ни к информатике (A = False), ни к физике (B = False), то и результат объединения будет ложным: False OR False = False. Не стоит полагаться на авось, если хочешь стать айтишником, придется готовиться.
Таким образом, дизъюнкция в булевой алгебре позволяет объединять различные условия или события и проверять, выполняется ли хотя бы одно из них.

Многозначная логика
Многозначная или нечеткая логика — раздел математики, который расширяет классическую бинарную логику, позволяя выражать неопределенность и нечеткость в логических высказываниях. В отличие от бинарной логики, в которой каждое высказывание может быть только истинным или ложным, в многозначной логике высказывание может иметь любое значение из заданного набора значений, называемого множеством истинности.
В многозначной логике дизъюнкция — это также логическая операция, которая используется для объединения двух или более высказываний. Однако, в отличие от классической логики, в многозначной логике дизъюнкция может принимать более двух значений.
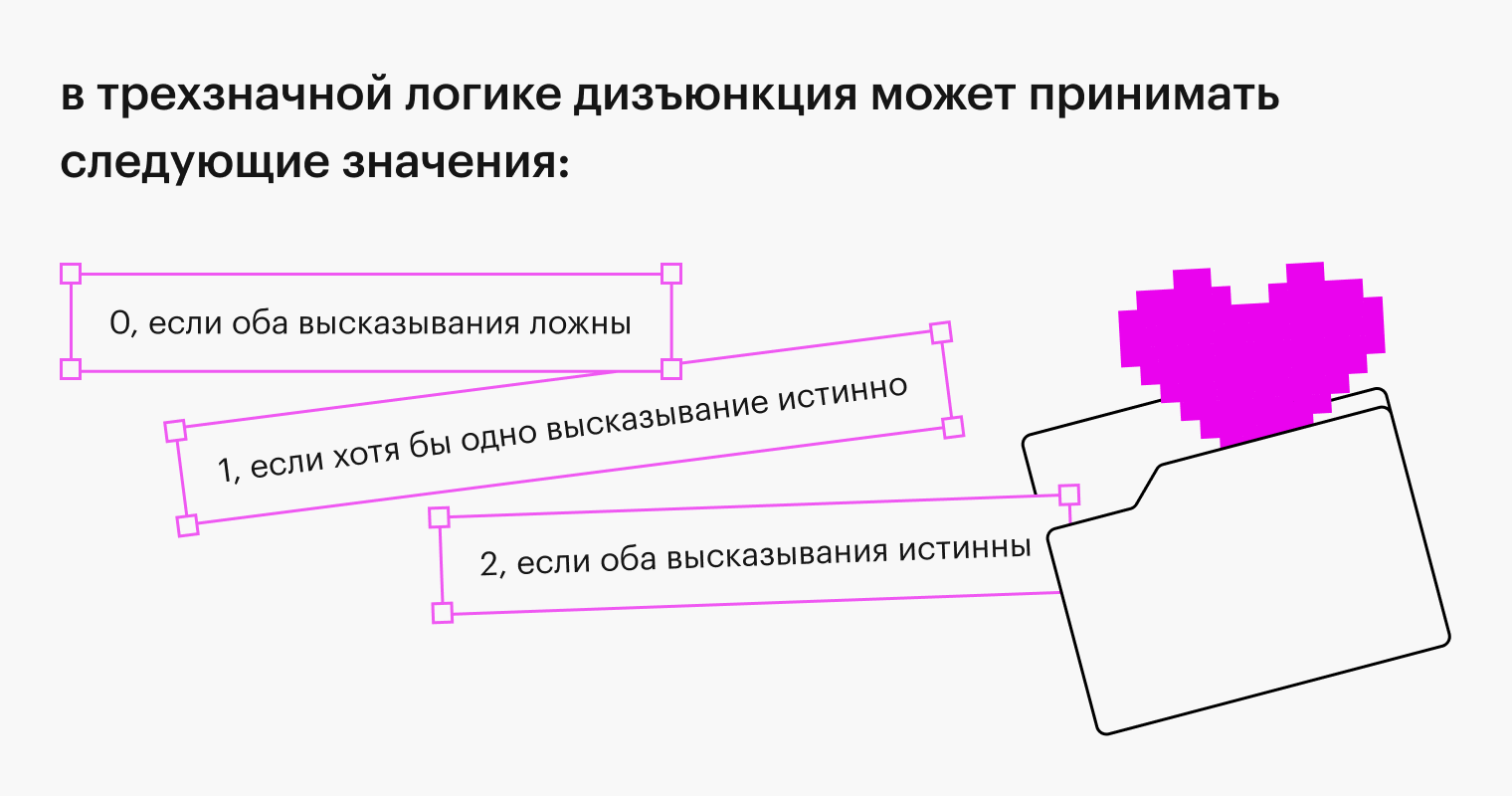
В трехзначной логике дизъюнкция может принимать следующие значения:
- 0, если оба высказывания ложны;
- 1, если хотя бы одно высказывание истинно;
- 2, если оба высказывания истинны.
Другие варианты многозначной логики могут иметь большее количество возможных значений дизъюнкции.
Пример
Представь, что нужно решить, сможешь ли ты пойти в кино в определенный день. Есть два условия, которые должны быть истинными, чтобы ты мог пойти:
- У тебя есть деньги на билет (A).
- Ты выучил все логические операции (B).
Будем использовать три варианта значений: истина (T), ложь (F) и неопределенность (U).
Объединим эти условия с помощью дизъюнкции. Если хотя бы одно из условий является истинным (T), то результат будет неопределенным. Таким образом, мы можем записать это с помощью дизъюнкции: (A) ИЛИ (B).
В таблице истинности для этой дизъюнкции в многозначной логике мы можем получить следующие комбинации значений:
- (T) или (T) = (T) (если у тебя есть деньги и ты выучил все логические операции, ты пойдешь в кино).
- (T) или (F) = (U) (если у тебя есть деньги, но ты не выучил все логические операции, тебя ждет неопределенность. Нужно больше времени уделить информатике, видимо!).
- (F) или (T) = (U) (жаль только, если ты выучил все логические операции, но у тебя нет денег, тебя тоже ждет неопределенность. А с «Соткой» смог бы и выучить все, и денег на кино сэкономить).
- (F) или (F) = (F) (конечно, если у тебя нет денег, и ты не выучил все логические операции, в кино ты не пойдешь. Селяви).
Таким образом, в многозначной логике дизъюнкция позволяет объединять условия и решать, выполняется ли хотя бы одно из них, в зависимости от заданных значений истинности, ложности и неопределенности.
Программирование
В программировании дизъюнкция (OR) — это логический оператор, который используется для объединения двух или более логических выражений, и результатом его выполнения является логическое значение true (истина), если оба или хотя бы одно из выражений истинно, и false (ложь), если все выражения ложны.
В большинстве языков программирования символ для оператора — две вертикальные черты (||).
Пример:
В языке Java выражение (x > 5 || y < 3) будет истинным, если хотя бы одно из двух условий (x > 5 или y < 3) будет выполнено.
В языке Python дизъюнкция может использоваться для более сложных выражений. Выражение (a > b) or (c < d) означает, что если a больше b или c меньше d, то результат будет истиной.
Принцип работы дизъюнкции в программировании тот же самый: если хотя бы одно условие выполняется, результат будет истинным, если все условия ложны, то и результат будет ложным.
Дизъюнкция может использоваться в условных операторах и циклах для принятия решений на основе логических выражений. Она также может быть полезна при обработке данных, когда необходимо выбрать данные из разных источников в зависимости от условий.
Связь с естественным языком
В жизни мы постоянно используем слова «или», «либо», «иначе», чтобы объединять несколько своих мыслей в одно высказывание, позволяет выбрать из предложенных вариантов. Так что в естественном языке дизъюнкция также ярко проявляется.
Пример
Выражение «Проверим себя или пойдем отдыхать» может быть интерпретировано как дизъюнкция двух высказываний: «Проверим себя», «Пойдем отдыхать». Если ты захочешь проверить себя, короткий тест ждет тебя ниже, если нужна передышка, отдыхай. Но не забудь вернуться к обучению.
В естественном языке принцип дизъюнкции действует так же: если одно из высказываний истинно, то всё выражение будет истинным.
Проверь себя
Дизъюнкция — это…
-логическое умножение;
-логическое сложение;
-неведомое нечто.
В большинстве языков программирования дизъюнкцию обозначают символом:
-«||»;
-«∑»;
-«∨».
Есть два высказывания: «Я будущий айтишник», «Этот тест слишком простой». Когда высказывание «Я будущий айтишник или этот тест слишком простой»?
-Когда ложно высказывание «Я будущий айтишник», но истинно «Этот тест слишком простой».
-Когда оба высказывания ложны.
-Я будущий айтишник, этот тест точно слишком простой.